Options Strategies: Delta Neutral

In a previous article we briefly covered the Greek called Vega and will give a deeper look into how Market Makers use the Greek Delta to inform their trading in this article. Delta is the derivative’s sensitivity to the price of the underlying. For example, assume you have a Delta of 1, for every move the underlying makes, your derivative (option price) will move $1. Having a Delta of 1 is unusual when trading options because it means you are very deep in the money. Options will usually have a Delta of 0.5 or below, a Delta of 0.5 means your strike price is close to where the underlying (Bitcoin) is trading at and anything lower means your option strike price is out of the money.

Side note: Delta is also an easy heuristic to use if you want to know the chance of your option expiring in the money. So if you have a Delta of 0.25, option traders might say they have a 25% chance of their option expiring in the money.

Here is a brief explanation of how Delta works to refresh your memory. Let’s assume we have a position of one Bitcoin Call with a Delta of 0.3.

BTC Price: $22,500

Delta: 0.3

Option Price: $350

Now let's assume Bitcoin increases in price to $22,501, our option price should then increase to $350.30 (the amount of Delta). But if Bitcoin were to decrease in value instead, our option would decrease by 30 cents (all else being equal). 

When looking at Delta it’s easy to tell how you want the underlying to trend, with a positive Delta you want the underlying to increase in price, and if you have a negative Delta you want the underlying to decrease in price. If the overall Delta of your portfolio is zero, you are what’s called Delta Neutral and the positions are structured to offset each other no matter which direction the underlying moves.

Let’s move on. Delta tells us how the value of our option will change as price changes, but as price changes, the Delta itself also moves. The question then becomes how do we measure the change in Delta itself with respect to the underlying?

Gamma is a second-order derivative that measures the change in Delta. It's easier to illustrate what's happening so let's go back to our example and add in Gamma.

BTC Price: $22,500

Delta: 0.3

Gamma: 0.005

Option Price: $350

Taking the same scenario from above, if the Bitcoin price increases by $1, our option value will increase by 30 cents, and now our Delta should increase by our Gamma to 0.305. If Bitcoin were then to increase by another dollar, the value of our option would again increase but by the new Delta of 0.305 (again, all else being equal). Secondly, we would be left with a new (increased) Gamma. It’s easier to think of Gamma a gas pedal, it tells Delta how fast or slow to increase or decrease in relation to the underlying price.

Why is this important? Some of the biggest participants in the space are liquidity providers, also known as Market Makers (MM). A Market Maker’s goal is to always be Delta Neutral, which means it’s helpful to know how much your Delta is going to move every time Bitcoin makes a jump in price.

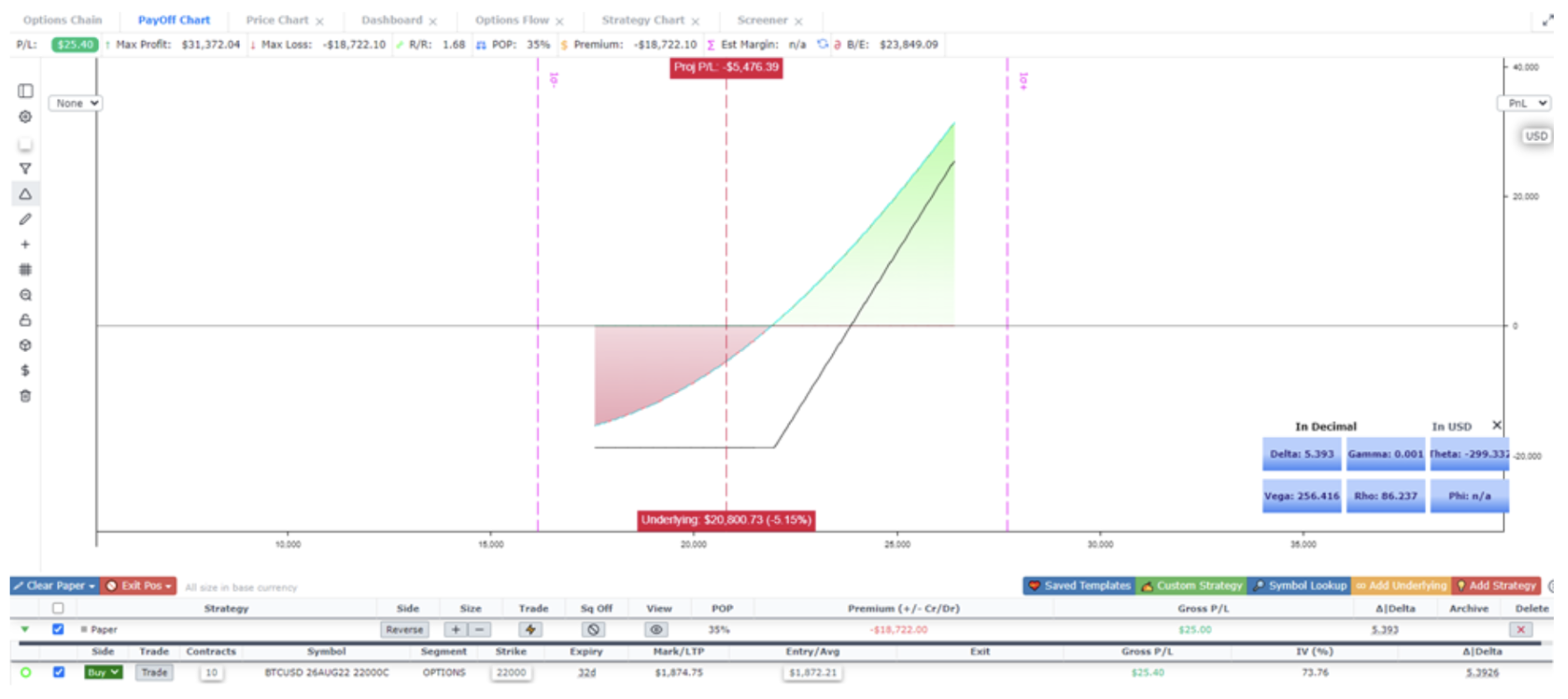
Now let’s crystalize this concept by looking at another example. Imagine a MM has 10 Calls on their book.

Long 10x Bitcoin Calls (Positive Delta)

BTC Price: $21,992

Call Delta: 5.39

Position Gamma: 0.001

With this position, the MM is long 5.39 Delta. If Bitcoin were to rally the MM would make money, but if Bitcoin were to dump in in price the MM would lose the entire premium paid for the Calls. If the MM wanted to bring their position to a neutral state they would simply need to sell 5.39 Bitcoin futures contracts. Let's take a step back now, one future represents 1 Bitcoin and moves in a 1:1 fashion, that’s why we call futures Delta 1 derivatives. So by selling 1 Bitcoin future representing 1 Bitcoin you are effectively offsetting 1 Delta of your position. 

If Bitcoin rocketed in price by $1000…

The new position Delta might have done something like this: 

Call Position Delta = 5.39 + (0.001*1000) = 6.39

Future Delta: -5.39

Position Delta = 6.39 + (-5.39) = 1 Delta

This looks as though the position has picked up 1 extra Delta. To bring themselves back to a neutral position the MM must sell one more futures contract. This is what's so interesting about being Delta Neutral, the astute among you may have noticed that if a MM has a book with a net positive Delta, as the price increases, they must sell Futures (or perps) to bring themselves back to a neutral position, and if the price is dipping the MM must do the opposite by buying back the Deltas they are losing. You can thus extrapolate that if MM’s have billions of dollars on their books, selling into rallies and buying dips can lead to a dampening of volatility. 

The opposite is true if a MM's book has a net negative Delta. The MM’s will need to sell into dips and buy into rallies, effectively exacerbating price movement. Let's look at the opposite side of the trade we put on earlier but this time let's say the MM sold 10 Calls.

Their book is now short or negative -5.39 Deltas. To offset the Delta, again we are going to immediately buy 5.39 futures contracts giving us a 0 Delta.

Using the same math as above, let's assume Bitcoin rallies $1,000 and then add our now negative Gamma to our negative Delta.

Call Delta = 0 + (-0.001*1000) = - 1

Position Delta = -1

It’s almost counter intuitive but as Bitcoin rallies the MM will lose one Delta (in our scenario), to get that Delta back they would need to buy one futures contract. Again, when the overall portfolio has negative Gamma, a MM will have to buy into rallies and sell into dips thus pushing the move further in the direction it’s heading.

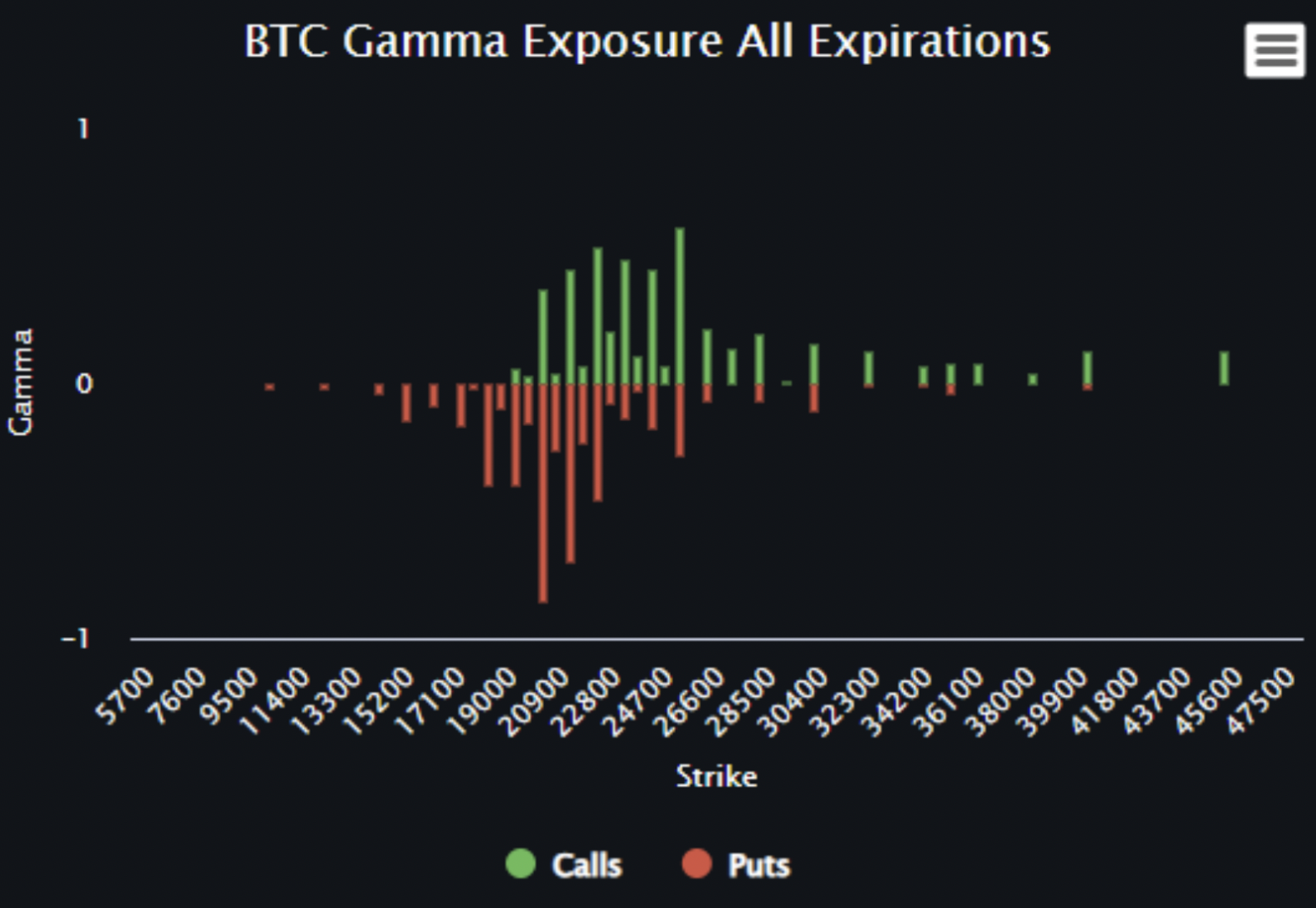
Accurately calculating how much Gamma is amalgamated on the MM’s books and whether it's negative or positive can pose a problem. Laevitas has built a tool that gives you a rough idea although the calculation makes some bold assumptions.

Assuming that the calculation was perfect, you would be able to accurately assume where MM’s are forced to buy into rallies and sell into dips if Gamma was negative. Or inversely, you could see where MM’s might have to sell rallies with a positive Gamma thus stifling the move and volatility overall.  

This is just one of many ways to dive a little deeper into how the options markets work. It’s simply an imperfect framework you can use in congruence with all the other available data we are so fortunate to have in crypto markets.